EL SONIDO: BASES FISICAS PARA SU APLICACIÓN EN ECOGRAFIA (Parte III)

Revista de Posgrado de la Cátedra VIa Medicina N° 105 - Junio/2001
Página: 17-21

EL SONIDO: BASES FISICAS PARA SU APLICACION EN ECOGRAFIA (Parte III)
Prof. Dr. Juan Fernando Gómez Rinesi

Efecto Doppler
    En los capítulos anteriores hemos analizado las características del fenómeno ondulatorio y los efectos que tienen los medios, en función de su impedancia, sobre la dirección y la energía portada por la onda de un emisor. Hemos observado entonces que la onda sufre modificaciones de velocidad de propagación y amplitud y que las interfases entre medios de distinta impedancia acústica desvían su trayectoria. Por el contrario, nada ocurre con su frecuencia.
    Para los casos en los que el emisor se halla en movimiento, la onda que es detectada por un receptor estático (quieto) no tendrá la misma frecuencia.
    Para comprender este fenómeno es necesario el repaso de algunos conceptos ya citados en las partes precedentes.

1) La velocidad de propagación de la onda en un medio determinado es constante.
2) La longitud de onda ( distancia recorrida por la onda para completar una oscilación completa) se expresa matemáticamente de la siguiente manera: (Ecuación 1)
Donde:
= longitud de onda
c = velocidad de propagación de la onda en el medio
f = frecuencia de la onda

Multiplicando numerador y denominador del segundo término de la Ecuación 1 por un mismo número, el resultado no varía. Para este caso: t correspondiente a un determinado tiempo la ecuación quedaría formada de la siguiente manera:

Pero como c es una velocidad y toda velocidad multiplicada por tiempo da distancia : c.t = d en tanto que f.t es el número de oscilaciones producidas en el tiempo t., reemplazando c.t por d tenemos:

(Ecuación 2)

Teniendo presente estos conceptos analizaremos los efectos que tienen sobre la frecuencia de la onda el acercamiento y/o alejamiento entre una fuente emisora de onda y una superficie reflectante. En la figura 1 se presentan las tres situaciones genéricas:

(a) Fuente y superficie reflectora se mantienen estáticas, por lo tanto, la distancia entre ellas no varía durante el tiempo t.
(b) durante el tiempo t, la distancia entre ambas disminuye(sea por movimiento de la fuente o de la superficie reflectora)
(c) durante t, la distancia entre ambas aumenta, también por movimiento de cualquiera de las dos. No obstante que, como se ha dicho, el efecto del alejamiento o el acercamiento entre fuente y superficie reflectante es independiente de cual de ellas se mueve, para facilitar la comprensión y aproximándonos a las aplicaciones de este efecto en el campo de la ultrasonografía diagnóstica , tanto al acercamiento como al alejamiento lo haremos a expensas del movimiento de la superficie reflectante (SR)

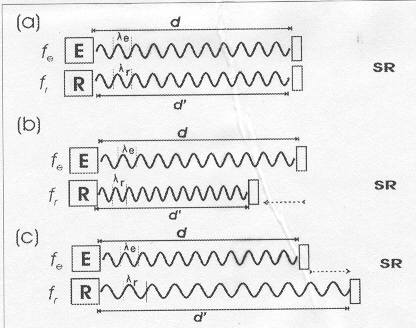
Figura 1: Modificaciones de la frecuencia: Efecto Doppler. Se representa el diagrama de un sistema de emisión-recepción de una onda donde E es la fuente emisora, SR la superficie reflectora de la onda y R el receptor de la onda reflejada, d mide la distancia inicial y d’ la correspondiente al final del intervalo t (ver texto). Las flechas de líneas punteadas representan el desplazamiento de la SR durante t. fe y fr representan la frecuencia emitida y la frecuencia de la onda reflejada, respectivamente. le y lr son las longitudes de onda emitida y reflejada.

En (a) la longitud de onda de la onda emitida(l_e) es, conforme a la ecuación 2, es:
y, por la misma razón , , como d y d’ son iguales porque no se a producido variación de distancia durante el tiempo t, resulta que ambas longitudes de onda son iguales, el número de oscilaciones emitidas durante el tiempo t ( fe . t) es igual al número de oscilaciones reflejadas(fr . t) durante ese mismo tiempo y teniendo en cuenta la ecuación 2 tenemos que:

y ; son f_e y f_r iguales.

Corolario 1: Si la distancia entre la fuente emisora y la SR no varía durante el tiempo t, la frecuencia de la onda emitida y la frecuencia de la reflejada son iguales durante dicho tiempo.
En el caso (b) de la figura 1, durante el tiempo t, la SR se aproxima a la fuente y por lo tanto disminuye la distancia d’ y por lo tanto d > d’, por lo que l_{e >}l_ry como la frecuencia de onda es inversamente proporcional a la longitud de onda (ecuación 2), resulta que f_e < f_r.

Corolario 2: Si la distancia entre la fuente emisora y la SR disminuye durante el intervalo t, la frecuencia de la onda reflejada es mayor que la de la onda emitida.
Finalmente, para el caso (c) de la figura 1, en el que la SR se aleja de la fuente emisora durante el tiempo t, resulta que d < d’ , por lo tanto, l_{e <}l_r y, entonces, f_e > f_r.

Corolario 3: Si la distancia entre la fuente emisora y la SR aumenta durante el intervalo t, la frecuencia de la onda reflejada es menor que la de la onda emitida.

Como acabamos de ver, es la "variación" de distancia en un determinado tiempo (velocidad) la que produce el cambio de frecuencia, cambio que es proporcional a la magnitud y dirección de esta variación que, en definitiva, es la velocidad de la SR para el caso estudiado, pero que bien podría ser la de la fuente emisora, si esta fuera la que se halla en movimiento.

A los cambios de frecuencia de onda producidos por el movimiento de una fuente emisora se denomina Efecto Doppler. Parecería un contrasentido haber presentado esta explicación con el movimiento de una superficie reflectora por cuanto, en realidad, al efecto se lo define en función del movimiento de la fuente emisora; pero resulta que, de acuerdo al principio de Huygens, toda superficie reflectora se comporta como una fuente emisora secundaria.

Se entiende por Frecuencia Doppler a la diferencia entre la frecuencia de la onda recibida y la onda emitida y se expresa:

Donde:
= Frecuencia Doppler.
= Frecuencia recibida.
= Frecuencia emitida.
Como la onda emitida depende de las características de la fuente emisora, en cuanto a la naturaleza y frecuencia no existen inconvenientes en conocerla. No ocurre lo mismo con la frecuencia de la onda recibida, es decir la que resulta del movimiento de la fuente la que debe ser calculada a partir de parámetros conocidos que intervienen en el fenómeno, a saber:

1) Frecuencia de emisión
2) Velocidad de Propagación de la onda en el medio
3) Dirección, velocidad y sentido del movimiento de la fuente. Una situación posible cuando se desea conocer la velocidad de una superficie reflectora (emisión secundaria) o una fuente emisora, frecuente en ultrasonografía Doppler, es que la dirección del haz ondulatorio emitido no coincida con la dirección del movimiento de la fuente. En ese caso, teniendo en cuenta que el movimiento es una magnitud vectorial y por tanto puede aplicarse la regla del paralelogramo, la velocidad con la que se acercan o se alejan emisor y receptor no refleja la velocidad que realmente tiene el móvil. Para explicar este fenómeno utilizaremos el ejemplo de la figura 2.

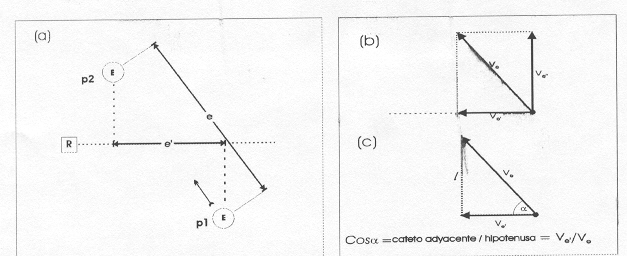
Figura 2. Cálculo de la velocidad de la fuente emisora cuando la dirección del movimiento es diferente a la dirección del haz ondulatorio recepcionado. En (a) la fuente emisora(E), durante un tiempo t, se desplaza en la dirección indicada por la flecha, desde la posición p1 hasta la posición p2 recorriendo la distancia e, por lo tanto la velocidad de E es : e/t. Durante este mismo tiempo, el acercamiento hacia el receptor (R) en el sentido que explora el haz ondulatorio ( linea de puntos finos) , el horizontal, solo se ha desplazado la distancia e’ y por lo tanto la velocidad con que se aproxima E a R es e’/t. Como puede advertirse los cambios de frecuencia reflejarán esta última velocidad, que es menor que la de E.
En (b) se muestra como puede descomponerse el movimiento de E, cuya velocidad, sentido e intensidad están representados por el vector Ve y la velocidad de acercamiento a R (e’/t) en el sentido horizontal (que es la dirección del haz ondulatorio) por el vector Ve’ y, finalmente, en (c) se construye un triángulo rectángulo cuya hipotenusa es el vector Ve y el cateto adyacente el vector Ve’ , de manera que que limitado el ángulo a que corresponde al ángulo de desviación entre la dirección del haz y la de el movimiento de E. Por trigonometría :

Teniendo en cuenta lo explicado en la figura 2, es posible conocer la velocidad de la fuente aplicando la fórmula del coseno del ángulo de desviación entre el movimiento de E y la dirección de exploración del receptor, de la siguiente manera:
si:

_{resulta, por pasaje de términos,
que:}

Esto explica la intervención del coseno del ángulo de desviación entre la dirección de recepción y la del desplazamiento de E en la fórmula general de frecuencia Doppler que sigue:

Donde :

f_D= Frecuencia Doppler
f_e= frecuencia de emisión
V_e= velocidad de E ( fuente emisora)
c = velocidad de propagación de la onda en el medio

BIBLIOGRAFIA

Taylor K, Burns P, Wells,P. Clinical aplications of doppler ultrasound.S4econd Editio. Raven Press.New York. 1995.
Marcus M, Schelbert H., Askorton D., Wolf G. Cardiac imaging. a companion to braunwald´s heart disease. 3^rd ed. W.B. Saunders Company. Philadelphia.1988.
Sears F, Zemansky M., Física general.Quinta edición.Aguilar. Madrid.1973
Miákishev G, Bújovsev. Física 4. Editorial Mir Moscú. Moscú. 1986
Miguel C. Física. 24ª. Edición. El ateneo.Buenos Aires.1993
Frumento A., Biofísica. Tercera edición.Mosby/Doyma Libros. Madrid.1995

Ir al Indice General Ir a la Tapa de la Revista Volver a la página de la Facultad